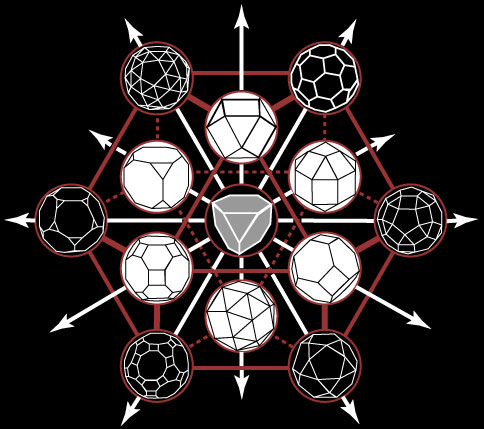
To be an Archimedian (a semi-regular solid) requires that all of its vertices lie in the surface of a circumscribing sphere (rust circles). Surrounding the truncted tetrahedron (grey faces) is the first set of six Archimedians (white faces) formed from the truncations of the regular octahedron. The outer six (black faces) are formed from the trunctions of the regular icosahedron. Together these 12 surround the center truncated tetrahedron (12 around 1 or closest packing) forming the cuboctahedron (rust colored lines). The top of the cuboctahedron is illustrated by the solid lines forming its four equilateral triange and three square faces and the bottom by the broken lines forming the remaining four triangle faces and three square faces. The 12 white vectors of Buckminster Fuller's Dymaxion (Vector Equilibrium) pass from the center of the truncted tetrahedron each one through one of its 12 vertices and on through each of the Archimedians residing at the 12 vertices of the cuboctahedron. The truncated tetrahedron is the only semi-regular solid figure with 12 independent axis ( The Twelve Degrees of Freedom) passing through its vertices from its center. As to the question of whether Existence is or is not a matter of randomness, PORCELAINia in more inclined to answer, "is not," given the information above.

Gratitude is given to Keith Critchlow and his book, "Order in Space" (Thames & Hudson, 1969) and to Bonnie DeVarco for making the book available to PORCELAINia. The above diagram and text is based on Critchlow's work found on pages 38 and 39 of his book.

Back to Main Page ARCHIMEDIA

ABOUT CONTACT CREDITS 2000 GALLERY

Site Map